Finance formulas

This page will give you a basic understanding of the following formulas commonly know as the six functions of a dollar:

• simple interest
• compounding
• discounting
• annuities
• sinking funds
• amortisation

Future value

Future value (FV) refers to the amount of money that an initial amount (PV) will grow to over some period of time (n) at a given interest rate (i).

There are two alternative methods of calculating interest on the initial amount. These are simple interest and compound interest.

Simple interest

The borrower pays the lender interest at regular periods within the term of the loan plus the principal and a single interest period payment at the end of the term. In this case interest accrues only on the original principal sum and does not compound.

The simple interest formula can be expressed as:

FV = PV x i x t

where PV is the amont of the present or current value
i is the interest rate
t is the number of periods

Compound interest

The borrower pays the lender a single sum at the end of the loan term. This sum includes the original principal plus interest on accumulated interest from previous periods.

Using the previous example:

You have borrowed $1,000 at 5% interest. Let us assume that you agree to repay the principal and interest after five years. Let us further assume that the interest is compounded annually. Your loan would look something like this after five years:

Original loan	$1,000.00
Interest year 1 Principal at the end of year 1	$50.00 $1,050.00
Interest year 2 Principal at the end of year 2	$52.50 $1,152.50
Interest year 3 Principal at the end of year 3	$55.12 $1,157.62
Interest year 4 Principal at the end of year 4	$57.88 $1,215.50
Interest year 5 Principal at the end of year 5	$60.77 $1,276.27

It should be noted that compound interest is simply a repeated application of simple interest to the new principal amount. In order to make a compound interest calculation reasonably quickly it is necessary to use the following formula which considerably reduces the calculations involved in the preceding example:

FV = PV(1+i)^t

Where FV is the future value
PV is the present/current value
i = interest rate
t = number of periods

Discounting – The present value of a single payment

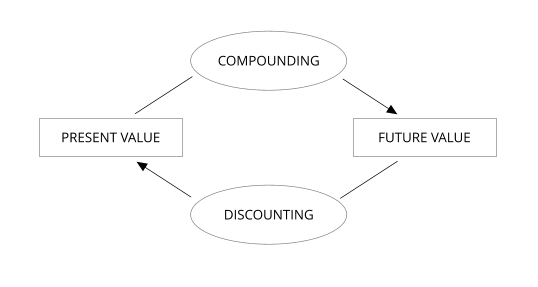
So far we have been interested in the problem of obtaining the future value of a principal sum. That is, given an initial investment and a certain interest rate, how much this initial investment will compound to over a specified time.

The above diagram illustrates that discounting involves the reverse of compounding. With discounting we are calculating the present value of a sum given a known future value.

As discounting is the reverse of compounding the discounting formula will simply be the inverse or reciprocal of the compounding formula. Thus:

To prove the relationship between compounding and discounting, let us take the present value sum of $1,366.0269 and compound this forward for four years at 10%. Thus:

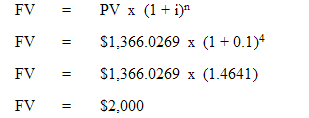
Annuities – Multiple periodic payments

When we are dealing with annuities we are considering a series of periodic payments that are usually, but not necessarily, equal in amount. With annuities we are faced with two problems: firstly, obtaining the future worth of an annuity, and secondly, obtaining the present worth of an annuity. Whereas with compounding and discounting we talk about a present or future lump sum payment, with annuities we are interested in a series of periodic payments.

Future value of an annuity

The future value of an annuity can be represented by the formula:

As interest is normally paid at the end of the period rather than at the beginning almost all the annuity tables are calculated on this basis.

For example: Let us suppose that an investor sets aside the sum of $100 every year at 5% interest rate. What will be the future worth of this sum in 20 years' time?

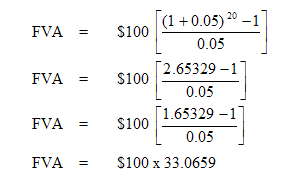
Present value of an annuity

This table is widely used in valuation and investment procedures to find the present value of a series of equal payments.

For example: The terms of a five year lease are such that there is a rental payment of $1,000 per annum. The problem is to ascertain the present worth of this income stream given an interest rate of 5%.

Using the formula:

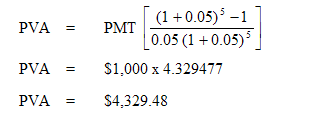
Sinking fund factor (amortisation of a future value)

This is used for working out the amount that will need to be set aside periodically so that, when compounded at a given interest rate, it will accumulate to a specified future sum.

This is the reciprocal of the future value of an annuity.

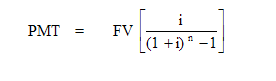
For example, let us suppose that an investor wants to accumulate $1,000 in five years and that the interest rate is 5%. How much does he/she need to set aside annually in order to accumulate $1,000 at the end of five years?

Using our formula:

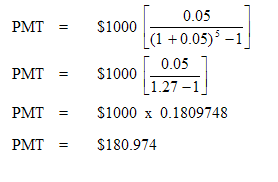
Thus, as the sinking fund factor is a reciprocal of the future value of an annuity, let us take an annuity of $180.974 and compound this forward at 5% per annum.

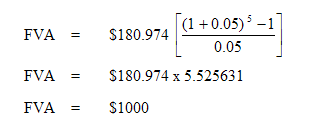
Partial payment (amortisation of a present value)

The purpose of this factor is to provide the period payments of capital and interest required to pay off or amortise a given principal sum in a given number of periods.

For example, if we have a 20 year table mortgage of $10,000 with a 10% interest rate, we need to be able to work out the annual payments of interest and principal. The factor that we derive, when multiplied by the original amount of the loan, will give us the annual installments of principal and interest. The formula for amortisation is the reciprocal of the present value of an annuity.

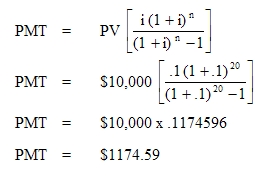
Thus, what is the present worth of an annuity of $1,174.59 per annum for 20 years using a 10% interest rate?

= $1,174.596 x 8.5136
= $10,000

Page authorised by Director - Centre for Learner Success
Last updated on 23 January, 2020